determinants.html

Systèmes linéaires et déterminants

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Exercice 1

> mat1:=matrix(5,5,[[-2,1,3,1,-2],[-2,-2,1,3,1],[1,-2,-2,1,3],[3,1,-2,-2,1],[1,3,1,-2,-2]]);

> inverse(mat1);

> det(mat1);

C'est ce qui explique le résultat si simple (sans fraction)...

Exercice 2

> matA:=matrix(3,3,[[1,1,m],[1,1,-1],[1,m,-1]]);

> factor(det(matA));

> solve({x+y+m*z=m,x+y-z=1,x+m*y-z=1},{x,y,z});

En fait, c'est lorsque le système est de Cramer; il reste faire les cas particuliers.

> m:=1:solve({x+y+m*z=m,x+y-z=1,x+m*y-z=1},{x,y,z});

> m:=-1:solve({x+y+m*z=m,x+y-z=1,x+m*y-z=1},{x,y,z});

Cela signifie non pas que Maple ne trouve pas de solution, mais qu'il n'en existe pas. Maple sait en effet résoudre les systèmes linéaires...

Exercice 3

> ?colspace

The functions rowspace(A) and colspace(A) return a set of vectors that form a basis for the vector space spanned by the rows and columns of the matrix A, respectively. The vectors are returned in a canonical form with leading entries 1.

> mat31:=matrix(4,1,[[0],[1],[1],[0]]);
kernel(mat31),colspace(mat31);

> mat32:=matrix(1,4,[[0,1,1,0]]);
kernel(mat32),colspace(mat32);

> mat33:=matrix(3,4,[[0,1,2,0],[1,0,1,0],[0,1,2,0]]);
kernel(mat33);colspace(mat33);

> mat34:=matrix(3,2,[[1,2],[3,4],[5,6]]);
kernel(mat34);colspace(mat34);

> mat35:=matrix(2,3,[[1,2,3],[4,5,6]]);

> kernel(mat35);colspace(mat35);rowspace(mat35);

Exercice 4

> mat41:=matrix(2,2,[[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]);

> kernel(mat41),colspace(mat41);

> det(mat41);

> simplify(%);

> mat42:=matrix(3,3,[[1,1,0],[2,2,1],[1,0,-2]]);

> kernel(mat42),colspace(mat42);

> mat43:=matrix(3,3,[[1,1,0],[2,2,0],[1,0,-1]]);

> kernel(mat43),colspace(mat43);

> mat44:=matrix(4,4,[[1,1,2,0],[0,2,-1,1],[0,0,3,2],[0,0,0,-1]]);

> kernel(mat44),colspace(mat44);

Exercice 5

> mat_5 := matrix([[1, cos(t_1), cos(2*t_1)], [1, cos(t_2), cos(2*t_2)], [1, cos(t_3), cos(2*t_3)]]);

> factor(det(mat_5));

Gloups ...

> combine(%,trig);

> expand(%);

> factor(%);

Sans les mains !

Exercice 7

> matA:=matrix(3,3,[[2*(a-1),2,-1],[2,2*a,2],[4*a,2*(2*a+1),2*a+1]]);

> factor(det(matA));

> solve({2*(a-1)*x+2*y-z=2*(a+1),2*x+2*a*y+2*z=4*a^2+3,4*a*x+2*(2*a+1)*y+(2*a+1)*z=16*a^3-2*a^2-a+5},{x,y,z});

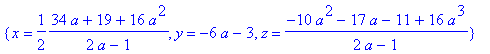
${x = 1/2*(34*a+19+16*a^2)/(2*a-1), y = -6*a-3, z = ...$

Les cas dégénérés ne sont pas traités. Attention, pour a=0 ou a=1, le résultat précédent est non grotesque mais faux : regardez par exemple l'exemple suivant :

> solve(a*x=a,x);

Pour a=0, tous les réels sont pourtant solution...

> a:=0:solve({2*(a-1)*x+2*y-z=2*(a+1),2*x+2*a*y+2*z=4*a^2+3,4*a*x+2*(2*a+1)*y+(2*a+1)*z=16*a^3-2*a^2-a+5},{x,y,z});

> a:=1:solve({2*(a-1)*x+2*y-z=2*(a+1),2*x+2*a*y+2*z=4*a^2+3,4*a*x+2*(2*a+1)*y+(2*a+1)*z=16*a^3-2*a^2-a+5},{x,y,z});

> a:=1/2:solve({2*(a-1)*x+2*y-z=2*(a+1),2*x+2*a*y+2*z=4*a^2+3,4*a*x+2*(2*a+1)*y+(2*a+1)*z=16*a^3-2*a^2-a+5},{x,y,z});

Pas de solution...

Exercice 8

> ?vandermonde

The function vandermonde(L) returns the Vandermonde matrix formed from the elements of the list. This square matrix has as its (i,j)-th entry L[i]^(j-1).

> VDM:=vandermonde([1515,exp(-1),pi]);