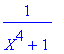
Fractions rationnelles
Accompagnement - corrigé

Exercice 1

1.1

> convert(1/(X^4+1),parfrac,X);

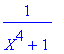
> convert(1/(X^4+1),parfrac,X,sqrt(2));

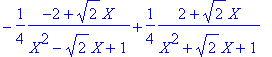
> convert(1/(X^4+1),parfrac,X,{I,sqrt(2)});

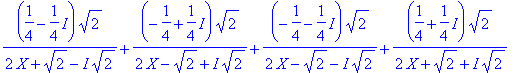
> ?alias

• Mathematics is full of special notations and abbreviations. These notations are typically encountered in written material as statements like ``let J denote the Bessel function of the first kind'' or ``let alpha denote a root of the polynomial x^3-2''. The purpose of the alias facility is to allow the user to state such abbreviations for the longer unique names that Maple uses and, more generally, to give names to arbitrary expressions.

> alias(alpha=RootOf(X^4+1));

> convert(1/(X^4+1),parfrac,X,{alpha});

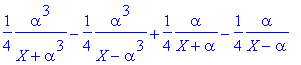
> convert(1/(X^4-1),parfrac,X);

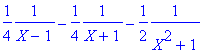
> alias(beta=RootOf(X^4+1));

> convert(1/(X^4-1),parfrac,X,{beta});

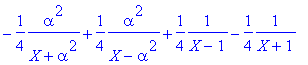
1.2

> convert(1/(1+X+X^2),parfrac,X);

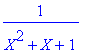
> alias(j=RootOf(X^2+X+1));

> convert(1/(1+X+X^2),parfrac,X,{j});

> convert(1/(X^8-1),parfrac,X,sqrt(2));

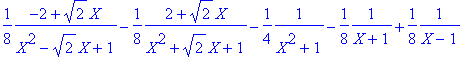
> alias(omega=RootOf(X^8-1));

> convert(1/(X^8-1),parfrac,X,{omega});

Error, (in evala) reducible RootOf detected. Substitutions are, {RootOf(_Z^8-1) = -1, RootOf(_Z^8-1) = RootOf(_Z^2+1), RootOf(_Z^8-1) = RootOf(_Z^4+1), RootOf(_Z^8-1) = 1}

> factor(X^8-1);

> convert(1/(X^8-1),parfrac,X,{alpha});

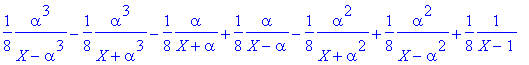
1.3

> convert(1/(X^2-2*cos(theta)+1),parfrac,X);

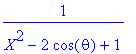
> alias(alpha=RootOf(X^2-2*cos(theta)+1));

Error, (in RootOf) expression independent of, _Z

> alias(alpha=RootOf(X^2-2*cos(theta)+1,X));

> convert(1/(X^2-2*cos(theta)+1),parfrac,X,{alpha});

Error, (in factor) 2nd argument is not a valid algebraic extension, {RootOf(_Z^2-2*cos(theta)+1)}

Mouais...

Exercice 2

> convert(1/((X^2-1)*(X^2+1)^2),parfrac,X);

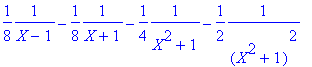
> convert(1/((X+1)^3*(X^2+X+1)^2),parfrac,X);

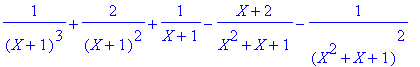
Sur C ca donnerait...

> alias(j=RootOf(X^2+X+1));

> convert(1/((X+1)^3*(X^2+X+1)^2),parfrac,X,{j});

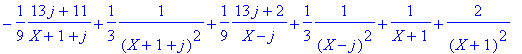
> F:=n->n!/product(X+k,k=1..n);

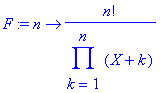
> for n from 1 to 8 do print(convert(F(n),parfrac,X)) od;

> seq(binomial(8,k),k=1..8);

> seq(k*binomial(8,k),k=1..8);

> convert((X^5+2)/(X^2+X+1)^3,parfrac,X);

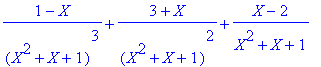
Sur C...

> convert((X^5+2)/(X^2+X+1)^3,parfrac,X,{j});

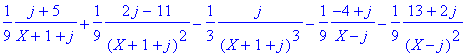
Exercice 3

> ?T

• The command with(orthopoly,T) allows the use of the abbreviated form of this command.
• The function T computes the nth Chebyshev polynomial of the first kind, evaluated at x.

> T(2,X);

> with(orthopoly);

> T(2,X);

> seq(convert(1/T(n,X),parfrac,X),n=1..5);

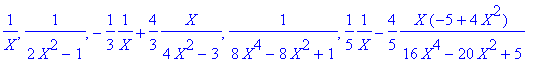
Ca ne peut rien donner de mieux...
En fait, Tn est de degré n, coefficient dominant 2^(n-1), et vérifie Tn(cos(theta))=cos((n+1)theta) pour tout theta, donc Tn admet n racines simples (lesquelles précisément ?). Il suffit ensuite de calculer des résidus...

Exercice 4

On écrit . F=P'/P vaut alors

Considérons maintenant une racine z de P' : si c'est une racine de P, c'est fini. Sinon, on peut évaluer F en z , ce qui donne la relation : =0, soit encore : =0

Ainsi, si a (qui est un réel >0), la relation =0 se traduit géométriquement par le fait que le point d'affixe z est barycentre des points d'affixes : gagné.

Exercice 5

> convert((X^2+X+1)/((X^2-1)*(X^2+1)),parfrac,X);

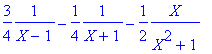
> convert(X/(X^4+X^2+1),parfrac,X);

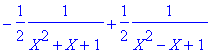
Exercice 6

> convert(7/((X+1)^7-X^7-1),parfrac,X);

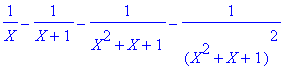
Vous vous attendiez à aussi simple ?