Feuille d'accompagnement TD :
algèbre linéaire et polynomes
Exercice 9
> P:=n->(X+1)^n-(X-1)^n:P(3);
![]()
> expand(");
![]()
> degree(",X),lcoeff(");
![]()
> degree(expand(P(1515)),X),lcoeff(expand(P(1515)));
![]()
> degree(expand(P(1789)),X),lcoeff(expand(P(1789)));
![]()
> Q:=n->(X^2+1)^n-(X^2-1)^n:Q(1515);
![]()
> degree(expand(Q(1515)),X),lcoeff(expand(Q(1515)));
![]()
> degree(expand(Q(1789)),X),lcoeff(expand(Q(1789)));
![]()
Exercice 10
>
horner:=proc(l,x)
local res,n,k;
n:=nops(l)-1; res:=l[n+1]; # res<-an
for k from 1 to n do #res<-res*x+a[n-k]
res:=res*x+l[n-k+1] od;
RETURN(res)
end;
![]()
![]()
![]()
![]()
> horner([1,3,-2,3,0,1],x);
![]()
> expand(");
![]()
Exercice 12
> with(orthopoly);
Warning, new definition for P
![]()
> seq(T(k,X),k=0..5);
![]()
> seq(U(k,X),k=0..5);
![]()
> subs(X=cos(theta),T(10,X));
![]()
> combine(",trig);
![]()
> subs(X=cos(theta),U(10,X));
![]()
> combine("*sin(theta),trig);
![]()
Exercices 13 et 14
> A:=X^6-4*X^3+2*X^2-1;B:=X^2+4;
![]()
![]()
> quo(A,B,X),rem(A,B,X);
![]()
> C:=4*X^3+X^2:D:=X+1+I:
Error, attempting to assign to `D` which is protected
D désigne l'opérateur de dérivation...
> C:=4*X^3+X^2:E:=X+1+I:
> quo(C,E,X),rem(C,E,X);
![]()
Exercice 23
> P:=n->X^(2*n+1)-(2*n+1)*X^(n+1)+(2*n+1)*X^n-1;
![]()
> subs(X=1,P(n));
![]()
> subs(X=1,diff(P(n),X));
![]()
> expand(");
![]()
> expand(subs(X=1,diff(P(n),X$2)));
![]()
> expand(subs(X=1,diff(P(n),X$3)));
![]()
> Q:=n->X^(2*n)-n^2*X^(n+1)+2*(n^2-1)*X^n-n^2*X^(n-1)+1;
![]()
> subs(X=1,Q(n));
![]()
> expand(subs(X=1,diff(Q(n),X)));
![]()
> expand(subs(X=1,diff(Q(n),X$2)));
![]()
> expand(subs(X=1,diff(Q(n),X$3)));
![]()
> expand(subs(X=1,diff(Q(n),X$4)));
![]()
Exercice 25
> P:=16*X^5-20*X^3+5*X-1;factor(P);
![]()
![]()
> solve(P);
![]()
On va dire à Maple de travailler sur un corps plus riche que Q, à savoir Q[sqrt(5)]...
> factor(P,{sqrt(5)});
![]()
> factor(P,complex);
![]()
Il s'agit d'une factorisation "numérique"
Exercice 26
X^8-1
> P:=X^8-1:factor(P);
![]()
Il s'agit en fait de la factorisation sur Q
> solve(P);
![]()
> factor(P,{sqrt(2)});
![]()
> factor(P,{sqrt(2),I});
![]()
X^8+X^4+1
> P:=X^8+X^4+1:
> factor(P);
![]()
> solve(P);
![]()
Pouah !!!!
> evalc({"});
![]()
> factor(P,sqrt(3));
![]()
> factor(P,{sqrt(3),I});
![]()
![]()
Exercice 30
> P:=X^3-4*X^2+2*X-1;
![]()
> sols:={solve(P)};
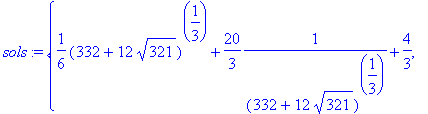
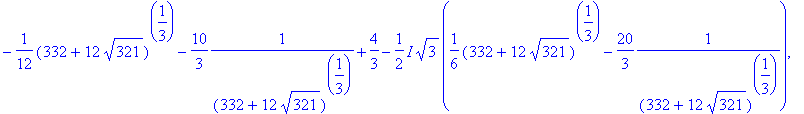
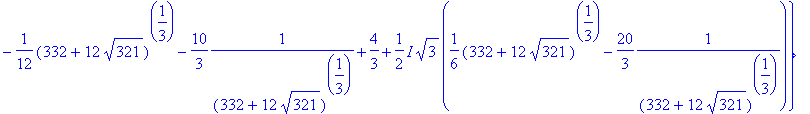
> sols[1]^2+sols[2]^2+sols[3]^2;
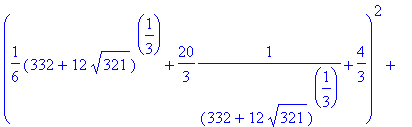
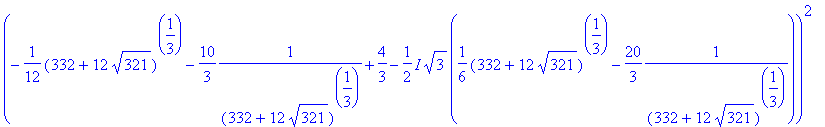
![]()
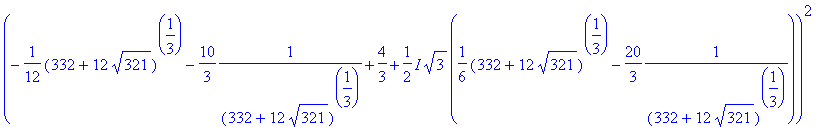
> expand(");
![]()
> sols[1]^3+sols[2]^3+sols[3]^3:
Résultat illisible...
> expand(");
![]()
> simplify(");
![]()
NB : lorsque Maple ne sait pas trouver explicitement les racines d'un polynôme, il peut cependant évaluer des expressions symétriques en ces racines, grâce RootOf, mais ça devient plus ardu...