TD : Dérivabilité des fonctions

numériques d'une variable réelle

Exercice 1

> f:=x->(sqrt(1+x)-sqrt(1-x))/x;

> plot(f,-1..1,0.9..1.5);

> limit((f(x)-1)/x,x=0);

> D(f)(x);

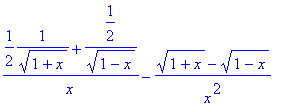
> limit(%,x=0);

Exercice 2

> diff(sqrt(1+sqrt(2+sqrt(x))),x);

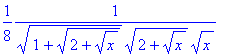
> diff(sqrt(1+sqrt(2+sqrt(x))),x);

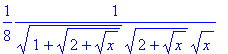
Il avait bon du premier coup !

Exercice 4

> diff(f1(x)*f2(x)*f3(x)*f4(x),x);

> D(f1*f2*f3*f4);

Exercice 7

> seq(diff(sin(x)^5,x$n),n=1..5);

> combine(sin(x)^5,trig);

> seq(diff(%,x$n),n=1..5);

> seq(diff(exp(x)*cos(x),x$n),n=1..10);

Exercice 8

> seq(diff(x^(n-1)*ln(x),x$n),n=1..12);

> seq((n-1)!,n=1..12);

Exercice 10

> limit((x-sin(x))/x^3,x=0);

> limit((ln(1+x)-x)/x^2,x=0);

Exercice 19

> taylor(sin(Pi/3+h),h=0,4);

Exercice 21

> taylor(1/(1+t),t=0,9);

> taylor(ln(1+t),t=0,10);

> taylor(1/(1+t**2),t=0,9);

> taylor(arctan(t),t=0,10);

> diff(arcsin(t),t);

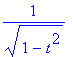
> taylor(%,t=0,7);

> taylor(arcsin(t),t=0,8);

Exercice 22

> DL:=proc(dernier)
local n,j,t;
t[0]:=0: t[1]:=1:
for n from 1 to dernier-1 do t[n+1]:=sum(t[j]*t[n-j],j=1..n)/(n+1) od;
RETURN(seq(t[n],n=0..dernier))
end:

> DL(10);

> taylor(tan(x),x=0);

> DL(18);

> taylor(tan(x),x=0,18);