Suites réelles

Exercice 2

> x:=n->binomial(2*n,n);

> limit(x(n)/x(n-1),n=infinity);

> x:=n->n^n/n!;

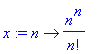
> limit(x(n)/x(n-1),n=infinity);

> x:=n->(3*n)!/(n^(2*n)*n!);

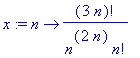
> limit(x(n)/x(n-1),n=infinity);

Exercice 6

> limit((2^(n+1)+3^(n+1))/(2^n+3^n),n=infinity);

> limit(sum(1/2^k,k=1..n),n=infinity);

> limit(sum((-1/3)^k,k=0..n),n=infinity);

> limit(n*sin(n!-1515)/(1+n^2),n=infinity);

> limit(sum(k^2,k=1..n)/n^3,n=infinity);

> limit(sqrt(1+n+n*ln(n))-sqrt(n),n=infinity);

> limit((n+(-1)^n)/(n-(-1)^n),n=infinity);

> limit((-1)^n*(2*(-1)^n+3),n=infinity);

> limit(simplify((-1)^n*(2*(-1)^n+3)),n=infinity);

Mouais...

> limit((-1)^n*(2*(-1)^n+3/sqrt(n)),n=infinity);

> limit(simplify((-1)^n*(2*(-1)^n+3/sqrt(n))),n=infinity);

> limit(sum(cos(1/sqrt(n+k)),k=0..n)/n,n=infinity);

Je suis bluffé...

> trunc(2.8);

> limit(sum(trunc(k*x),k=1..n)/n^2,n=infinity);

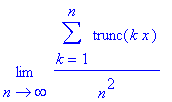
> add(trunc(k*Pi),k=1..1000)/1000^2;

> evalf(%);

Ca me rappelle quelque chose...

> 2*%;

> add(trunc(k*Pi),k=1..10000)/10000^2;

> evalf(%);

> 2*%;

> evalf(Pi);

La convergence semble assez lente.

Exercice 7

> rsolve({u(0)=-1,u(n+1)=2*u(n)-3},u(n));

> limit(%,n=infinity);

> rsolve({v(0)=2,v(n+1)=v(n)/2+6},v(n));

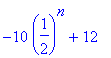
> limit(%,n=infinity);

> rsolve({w(0)=0,w(n+1)=-w(n)+2},w(n));

> limit(%,n=infinity);

Exercice 8

> a:=n->r*n+a0;

> a(1515);

> sum(a(k-1)*a(k)*a(k+1),k=1..n);

> limit(%/a(2*n+2)^4,n=infinity);

Exercice 9

> premiers_termes:=proc(n,u0)
local i,u,s;
u:=u0:s:=u:
for i from 1 to n do u:=1515+sqrt(u):s:=s,u od;
RETURN(s) end;

> premiers_termes(5,1024);

oops ! Il va falloir feinter...

> premiers_termes(5,1024.);

> Digits:=50;

> premiers_termes(10,1024.);

> premiers_termes_bis:=proc(n,v0)
local i,v,s;
v:=v0:s:=v:
for i from 1 to n do v:=v^2/(1+v^2):s:=s,v od;
RETURN(s) end;

> premiers_termes_bis(5,1515);

oops again !

> Digits:=10:premiers_termes_bis(10,1515.);

Exercice 11

> asympt(n*(n^(1/n)-1),n);

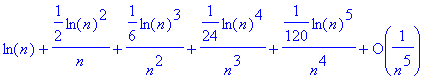
> asympt(n*(n^(1/n)-1),n,1);

> asympt(sqrt(n^2+1789*n+1515)-n,n,1);

> asympt((n^1515+1789)^(1/n),n,1);

> asympt(sum(1/k^k,k=1..n),n);

Error, (in asympt) unable to compute series

> asympt(sum(k^k,k=1..n),n);

Error, (in asympt) unable to compute series

> asympt(sum(k!,k=1..n),n);

Error, (in asympt) unable to compute series

> asympt(1-cos(alpha/n),n,3);

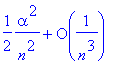
> asympt(n*(sin(1/n)-tan(1/(2*n))),n);

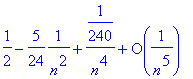
> asympt(tan(sin(1/n))-sin(tan(1/n)),n);

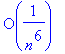
> asympt(tan(sin(1/n))-sin(tan(1/n)),n,8);

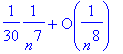
Exercice 12

Où le taupin surpasse Maple

> sum(k^1515,k=0..n);

Warning, computation interrupted

> sum(k^20,k=0..n);

> asympt(Sum(k^1515,k=0..n),n);

> asympt(Sum(k^100,k=0..n),n);

> asympt(Sum(k^500,k=0..n),n);

Où Maple m'étonne...

> limit(sum(1/(k*(ln(k)+1024)),k=1..n),n=infinity);

> asympt(sum(1/(k*(ln(k)+1024)),k=1..n),n,1);

Exercice 13

> u:=n->n^(ln(n)^2):v:=n->(n^2)^(ln(n)):w:=n->(ln(n))^(n*ln(n)):z:=n->(n*ln(n))^n:

> limit(u(n)/v(n),n=infinity);

> limit(w(n)/u(n),n=infinity);

> limit(w(n)/z(n),n=infinity);

> limit(z(n)/u(n),n=infinity);

Ainsi, v << u << z << w

Exercice 14

> alpha:=n->(ln(ln(n)))^(-ln(n*ln(n)));beta:=n->(ln(n*ln(n)))^(-ln(ln(n)));

> limit(alpha(n)/beta(n),n=infinity);

Ainsi, alpha << beta