Groupe orthogonal : TD

> restart:with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Exercice 4

> f:=vector([2,1]):x:=vector([x1,x2]):

> solve(dotprod(x-a*f,f)=0,{a});

> assign(%);

> evalm(x-2*a*f);

> genmatrix(convert(%,list),[x1,x2]);

C'est bien une matrice orthogonale, symétrique, de trace nulle.

Exercice 5

> a:=vector([3,4]):b:=vector([1,-2]):

> arccos(dotprod(a,b)/sqrt(dotprod(a,a)*dotprod(b,b)));

> det(matrix([a,b]))/sqrt(dotprod(a,a)*dotprod(b,b));

Donc l'angle orienté est arccos(1/sqrt(5))-Pi

Exercice 8

> A:=<<3 | -4> , <4 | 3>>/5:B:=<<3 | 4> , <4 | -3>>/5:

> evalm(A&*transpose(A)),evalm(B&*transpose(B));

> det(A),det(B);

A est donc une rotation et B une symétrie par rapport à :

> kernel(B-Matrix(2,shape=identity));

Exercice 9

> x:=vector([x1,x2,x3]):a:=vector([a1,a2,a3]):b:=vector([b1,b2,b3]):

> evalm(crossprod(a,x)-b);

> solve(%[1],{x1,x2,x3});

Mouais... a voir... Si b est non nul et colinéaire à a, l'équation initiale n'a clairement pas de solution : Maple a du faire des simplification illicites... c'est-à-dire diviser par quelque chose de potentiellement nul. Il faut donc reprendre cela à la main.

Exercice 11

Faisons cela tout en finesse...

> u:=vector([u1,u2,u3]):v:=vector([v1,v2,v3]):w:=vector([w1,w2,w3]):s:=vector([s1,s2,s3]):

> dotprod(crossprod(u,v),crossprod(w,s),orthogonal);

> dotprod(u,w,orthogonal)*dotprod(v,s,orthogonal)-dotprod(u,s,orthogonal)*dotprod(v,w,orthogonal);

> %-%%;

> simplify(%);

C'est bien la géométrie, non ?

> evalm(crossprod(crossprod(u,v),crossprod(w,s))-det(matrix([u,v,s]))*w+det(matrix([u,v,w]))*s);

> simplify(%);

héhé ! Bon, cela dit, on demande une preuve "humaine" de ces résultats...

Exercice 12

Essayons une méthode brutale en calculant dans une b.o.n.d obtenue par orthonormalisation...

> a:=vector([alpha,0,0]):b:=vector([beta,gamma,0]):c:=vector([delta,lambda,mu]):

> x:=vector([x1,x2,x3]):y:=vector([y1,y2,y3]):z:=vector([z1,z2,z3]):

> evalm(crossprod(x,y)-c);

> op(convert(%,list));

> e1:=%:

> e2:=op(convert(evalm(crossprod(y,z)-a),list));

> e3:=op(convert(evalm(crossprod(z,x)-b),list));

> solve({e1,e2,e3},{x1,x2,x3,y1,y2,y3,z1,z2,z3});

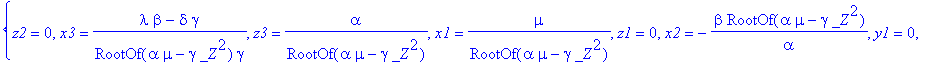
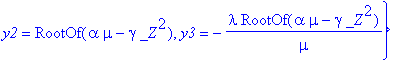
Très franchement je n'y croyais pas beaucoup...
alpha, gamma et mu étant non nuls, le résultat a au moins une petite chance d'être correct. Cela dit, on ne sait pas si dans son calcul, Maple n'a pas divisé par quelque chose de potentiellement nul. Il reste donc du travail.
On sait au moins ce qu'on veut montrer : z est colinéaire à "a vectoriel b", et par rôle symétrique, x et y sont respectivement colinéaires à "b vectoriel c" et "a vectoriel c". Quelques doubles produits vectoriels devraient permettre d'établir celà !

Exercice 13

> v1:=vector([1,1,0]):v2:=vector([1,0,-1]):v3:=vector([3,4,0]):

> arccos(dotprod(v1,v2)/sqrt(dotprod(v1,v1)*dotprod(v2,v2)));

> arccos(dotprod(v1,v3)/sqrt(dotprod(v1,v1)*dotprod(v3,v3)));

> arccos(dotprod(v2,v3)/sqrt(dotprod(v2,v2)*dotprod(v3,v3)));

> evalf(%+%%);

> evalf(Pi/3);

Exercice 14

> f:=vector([2,1,0]):x:=vector([x1,x2,x3]):

> solve(dotprod(x-a*f,f)=0,{a});

> assign(%);

> evalm(x-2*a*f);

> genmatrix(convert(%,list),[x1,x2,x3]);

C'est bien une matrice orthogonale, symétrique, de trace 1, qui stabilise e3 (qui est orthogonal à f)

Exercice 15

> generateur_exo:=proc(v0,theta)
local v,nv0,x,y,z;
v:=vector([x,y,z]):nv0:=sqrt(dotprod(v0,v0,orthogonal)): RETURN(genmatrix(convert(evalm(dotprod(v,v0,orthogonal)/nv0^2*v0+cos(theta)*(v-dotprod(v,v0,orthogonal)/nv0^2*v0)+sin(theta)*crossprod(v0,v)/nv0),list),[x,y,z]))
end:

> generateur_exo(vector([1,0,1]),Pi/2);

> generateur_exo(vector([1,0,-1]),Pi/3);

Exercice 16

> analyse_rotation:=proc(A)
local v0,theta,w:
v0:=op(kernel(A-Matrix(3,shape=identity))):
theta:=arccos((trace(A)-1)/2);
if v0[1]=0 then w:=vector([1,0,0]) else w:=vector([v0[2],-v0[1],0]) fi:
if evalf(dotprod(A&*w,crossprod(v0,w)))>0 then RETURN(evalm(v0),theta) else RETURN(evalm(-v0),theta) fi
end:

> A:=<<8 | 1 | -4> , <-4 | 4 | -7> , <1 | 8 | 4>>/9;

> evalm(A&*transpose(A));

> det(A);

> analyse_rotation(A);

> B:=<<3 | 1 | sqrt(6)> , <1 | 3 | -sqrt(6)> , <-sqrt(6) | sqrt(6) | 2>>/4;

> evalm(B&*transpose(B));

> det(B);

> analyse_rotation(B);

> C:=<<3 | 1 | sqrt(6)> , <1 | 3 | -sqrt(6)> , <sqrt(6) | -sqrt(6) | -2>>/4;

> evalm(C&*transpose(C));

> det(C);

Normal : on a changé L3 en -L3 dans B !

> kernel(C-Matrix(3,shape=identity));

> kernel(C+Matrix(3,shape=identity));

C est donc une réflexion.
N.B. :

- Le calcul du second noyau était inutile; pourquoi ?
- En fait, C étant symétrique, c'était forcément une réflexion (pourquoi ?)

> D:=<<8 | -1 | -4> , <-4 | -4 | -7> , <1 | -8 | 4>>/9;

Error, attempting to assign to `D` which is protected

Classique : D est l'opérateur de dérivation...

> DD:=<<8 | -1 | -4> , <-4 | -4 | -7> , <1 | -8 | 4>>/9;

DD est obtenu en changent C2 par con opposée dans A : DD va donc être orthogonale de déterminant -1.

> evalm(DD&*transpose(DD));

> det(DD);

DD n'est pas symétrique donc ne correspond pas à une réflexion : le premier calcul va le confirmer.

> kernel(DD-Matrix(3,shape=identity));

Déterminons l'axe de la rotation (qui est aussi l'orthogonal du plan de réflexion).

> kernel(DD+Matrix(3,shape=identity));

> f:=op(%);

> theta:=arccos((trace(DD)+1)/2);

On oriente l'axe par f. On va regarder l'image d'un vecteur v du plan : est-elle "du coté de "f vectoriel v" ?

> v:=vector([5,-1,0]):dotprod(crossprod(f,v),DD&*v);

Le sinus est donc négatif. Pour vérification...

> %/dotprod(v,v)/sqrt(dotprod(f,f));

> %^2+(17/18)^2;

Ouf ! (sauriez-vous expliquer le calcul ???)

Ainsi, DD est la réflexion par rapport à l'orthogonal de f, composée avec la rotation d'axe dirigé et orienté par f et d'angle -arccos(17/18).

Exercice 17

> evalm(crossprod(vector([a,b,c]),vector([x1,x2,x3])));

> genmatrix(convert(%,list),[x1,x2,x3]);