Méthode d'Euler

Tracé de polygones

> plot([[1,2],[2,5],[-1,6]]);

> plot([seq([n*Pi/5,sin(n*Pi/5)],n=0..10)]);

Méthode d'Euler sur un exemple simple

La méthode proprement dite

> euler:=gnagna;

Error, attempting to assign to `euler` which is protected

comprendo english ?

> eulerrr:=proc(f,N,pas,y0)
local k,s,y;
y:=evalf(y0):s:=y0;
for k from 0 to N-1
do
y:=y+f(y)*pas:s:=s,y
od;
RETURN([s])
end:

> eulerrr(t->t,10,.1,1);

Toolbox

Il faut générer la suite de polygones

> moulinette:=(l,pas,t0)->[seq([t0+k*pas,l[k+1]],k=0..nops(l)-1)];

> moulinette(eulerrr(t->t,10,.1,1),.1,0);

> plot(%);

Comparaison avec la vraie solution

> with(plots):

Warning, the name changecoords has been redefined

> display(plot(moulinette(eulerrr(t->t,10,.1,1),.1,0)),plot(exp,0..1,color=blue));

Résolution numérique de maple

> ?numeric

• Invoking the dsolve function with the numeric or type=numeric option causes dsolve to find a numerical solution for the ODE or ODE system. If the optional equation method= numericmethod is provided (where numericmethod is one of rkf45 , rosenbrock , bvp , dverk78 , lsode , gear , taylorseries , or classical ), dsolve uses that method to obtain the numerical solution.

• Both initial and boundary value problems can be numerically solved. For a system input, the type of problem is automatically detected.
• By default, a procedure is returned that can be used to obtain solution values if given the value of the independent variable.

• The default for initial value problems (IVP) is a Runge-Kutta Fehlberg method which produces a fifth order accurate solution (see rkf45 or numeric,IVP for more details). For boundary value problems (BVP), a finite difference technique with Richardson extrapolation is used (see numeric,BVP for more detail).

NDLR : la méthode de Runge-Kutta est grosso-modo une amélioration TRES sensible de la rustique méthode d'Euler

> f:=dsolve({D(y)(t)=y(t),y(0)=1},y(t),type=numeric,range=0..1);

> ?odeplot

• The odeplot function plots a solution curve (either 2-D or 3-D) determined from the output of a call to dsolve/numeric.

> odeplot(f);

> display(plot(exp,0..1,color=blue),odeplot(f));

Elles sont confondues...

> comparaison_euler:=proc(f,t0,y0,N,pas)
local y;
y:=dsolve({D(y)(t)=f(y(t)),y(t0)=y0},y(t),type=numeric,range=t0..t0+N*pas);
RETURN(display([plot(moulinette(eulerrr(f,N,pas,y0),pas,t0),color=blue),odeplot(y)]))
end;

Influence du pas...

> comparaison_euler(t->t,0,1,5,1);

> comparaison_euler(t->t,0,1,10,.5);

> comparaison_euler(t->t,0,1,100,.05);

> comparaison_euler(t->t,0,1,1000,.005);

Trois nouveaux exemples

Une fonction "qui explose"

> dsolve({D(y)(t)=exp(y(t)),y(0)=0},y(t));

> comparaison_euler(exp,0,0,10,.09999);

> comparaison_euler(exp,0,0,100,.009999);

> comparaison_euler(exp,0,0,1000,.0009999);

Un cas "sans solution simple"

> dsolve({D(y)(t)=sin(y(t)),y(0)=1},y(t));

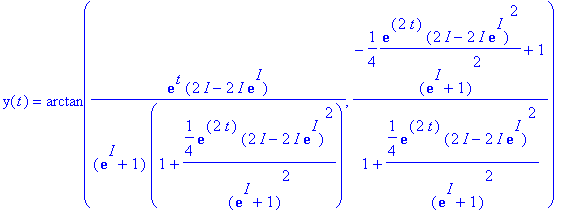
> simplify(%);

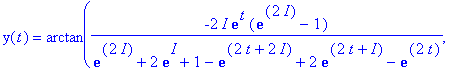
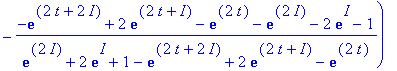
> comparaison_euler(sin,0,1,10,2);

> comparaison_euler(sin,0,1,20,1);

Un dernier pour la route

> dsolve({D(y)(t)=exp(sin(y(t))),y(0)=0},y(t));

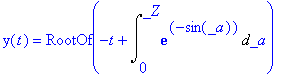
> comparaison_euler(t->exp(sin(t)),0,0,100,1);

> comparaison_euler(t->exp(sin(t)),0,0,1000,.1);

>

Même Runge et Kutta réunis ont du mal...

> dsolve({D(D(y))(t)-y(t)=0,y(0)=1,D(y)(0)=-1},y(t));

> f:=dsolve({D(D(y))(t)-y(t)=0,y(0)=1,D(y)(0)=-1},y(t),type=numeric);

> display({odeplot(f,0..1),plot(exp(-t),t=0..1,color=blue)});

Jusque là ça va (les deux courbes sont confondues)...

> display({odeplot(f,0..10),plot(exp(-t),t=0..10,color=blue)});

Exercice : expliquer !