Initiation aux DL

Pour avoir une limite avec Maple, on utilse la fnction "limit". Pour un équivalent et/ou un développement limité, on utilise en général "taylor", ou "series" si "taylor" n'y arrive pas. Si l'affaire se passe au voisinage de l'infini, on peut utiliser "asympt"

> ?limit

• The limit(f,x=a,dir) function attempts to compute the limiting value of f as x approaches a .
• If dir is not specified, the limit is the real bidirectional limit, except in the case where the limit point is infinity or -infinity , in which case the limit is from the left to infinity and from the right to -infinity . For help with directional limits see limit[dir] .

> ?taylor

• The function taylor computes the Taylor series expansion of expr, with respect to the variable x, about the point a, up to order n.
• The taylor function is a restriction of the more general series function. See series for a complete explanation of the parameters.

> ?asympt

• The function asympt computes the asymptotic expansion of f with respect to the variable x (as x approaches infinity).
• The third argument n specifies the truncation order of the series expansion. If no third argument is given, the value of the global variable Order (default Order = 6) is used.

Exercice 3

> limit((1-2/n)^(3*n),n=infinity);

Exercice 7

> limit((1-1/n)^n,n=infinity);

Exercice 13

> plot({x,x^2,sqrt(x)},x=0..1);

> plot({1/x,1/x^ 2,-ln(x)},x=0..1,0..5);

Exercice 14

> plot({x,x^2,sqrt(x),ln(x)},x=1..3);

> plot({1/x,1/x^2},x=1..3);

Exercice 15

> limit((1-2/n)^(3*n),n=infinity);

Incroyable !

Exercice 16

> taylor(1/sin(x)-1/x,x=0);

C'est un "développement de Taylor" (théorie en cours d'année). Le premier terme nous donne l'équivalent.

Exercice 17

> taylor(1/sin(x)^2-1/x^2,x=0);

> limit(1/sin(x)^2-1/x^2,x=0);

Exercice 20

> limit((t^t-1)/(1-t+ln(1+t)),t=1);

> limit(ln(t)/(t-1),t=1);

> limit((1-1/(n*sqrt(n)))^(n^(5/3)),n=infinity);

un peu plus subtil

> limit((t^t-1)/(1-t+ln(t)),t=1);

> limit((t^t-1)/(1-t+ln(t)),t=1,right);

> limit((t^t-1)/(1-t+ln(t)),t=1,left);

> taylor((t^t-1)/(1-t+ln(t)),t=1);

Error, does not have a taylor expansion, try series()

> series((t^t-1)/(1-t+ln(t)),t=1);

> limit(x^(sqrt(x))/(sqrt(x))^x,x=infinity);

> limit((Pi/2-x)^(sin(x)/ln(cos(x))),x=Pi/2);

> limit(tan(x)^(tan(2*x)),x=0);

Exercice 21

> limit(1/(1-x^x)-1/(x*ln(x)),x=0,right);

> limit(sqrt(x+sqrt(x))-sqrt(x),x=infinity);

> limit(cos(x)^(1/cotan(x)^2),x=0);

> limit(cos(x)^(1/tan(x)^2),x=0);

?????

> cotan(Pi/4);

Il n connait pas cette fonction... cela dit, il est "assez contestable" de donner la réponse qu'il donne sur limit(cos(x)^(1/cotan(x)^2),x=0)...

> limit(tan(x)^(tan(2*x)),x=Pi/2,left);

> limit(tan(x)^(tan(2*x)),x=Pi/4);

Exercice 22

22.1

> limit(1/cos(x)^2+1/ln(sin(x)^2),x=Pi/2);

> taylor(ln(sin(x)^2)+cos(x)^2,x=Pi/2);

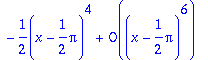
Soit encore :

> taylor(ln(sin(Pi/2+u)^2)+cos(Pi/2+u)^2,u=0);

22.2

> limit((x^sin(x)-sin(x)^x)/(x^tan(x)-tan(x)^x),x=0);

> taylor(x^sin(x)-sin(x)^x,x=0);

Error, does not have a taylor expansion, try series()

> series(x^sin(x)-sin(x)^x,x=0,4);

> series(x^tan(x)-tan(x)^x,x=0,4);

22.3

> limit((2^x+3^x-12)^(tan(Pi/4*x)),x=2);

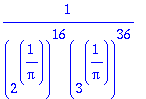
> simplify(%);

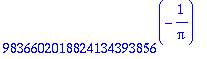
mouais...

22.4

> limit((exp(1)-(1+1/x)^x)^(sqrt(x^2+1)-sqrt(x^2-1)),x=infinity);

> taylor(exp(1)-(1+1/x)^x,x=infinity,2);

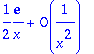
> taylor(sqrt(x^2+1)-sqrt(x^2-1),x=infinity,2);

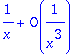
Exercice 23

> series(ln(tan(x)),x=0,1);

> taylor(ln(tan(x)),x=Pi/4,2);

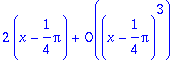
> series(sqrt(x^2+x)-(x^3+2*x^2)^(1/3),x=0,1);

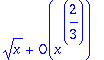
> asympt(sqrt(x^2+x)-(x^3+2*x^2)^(1/3),x,2);

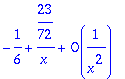
> series(1/x-1/tan(x),x=0,4);

> asympt(exp(1/x)-x*(x+1)/x^2,x,3);

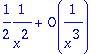
> asympt(sqrt(ln(2*n+1))-sqrt(ln(2*n)),n,2);

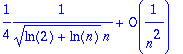
> asympt((ln(n+1)/ln(n))^n-1,n,1);

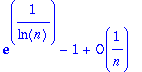
> simplify(%);

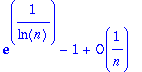
Etrange... je n'ai pas réussi à lui faire "voir" que exp(1/ln(n))-1 est équivalent à 1/ln(n). Comme quoi...

Exercice 24

> asympt((ln(x)/ln(x-1))^(x^2),x,1);

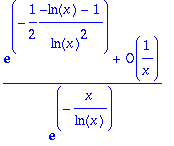
Arf ! On fait le calcul à la main... et onpeut tout de même vérifier :

> limit(exp(-x/ln(x))*(ln(x)/ln(x-1))^(x^2),x=infinity);

> asympt(exp(sqrt(x^2+x+1)),x,1);

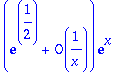
> expand(%);

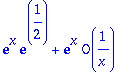
O(1/x) est uu terme qui tend vers 0, donc le tout est équivalent à exp(x)exp(1/2)

> series(exp(tan(x)^2),x=Pi/2);

Error, (in series/exp) unable to compute series

> series(tan(x)^2,x=Pi/2);

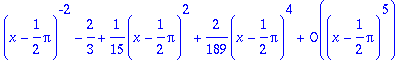
"donc" exp(tan^2(Pi/2+u)) est equivalent à exp(-2/3)exp(1/u^2)

> asympt(ln(n)/n-ln(n)^2/2+ln(n-1)^2/2,n,3);

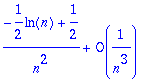
> asympt((ln(x)/ln(x-1))^(x^2),x,2);

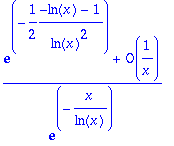
> simplify(%);

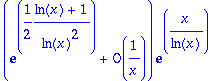
A la main :

> asympt(ln(x)/ln(x-1),x,3);

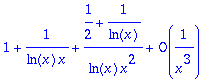
> asympt(x^2*ln(ln(x)/ln(x-1)),x,1);

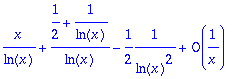
Et donc...

> series(x^x-(sin(x))^x-x^3/6,x=0,5);