TD : Réels

Feuille d'accompagnement

Exercice 2

> plot(3*x^2+26*x+35,x=-9..0);

> solve(3*x^2+26*x+35>=0);

Exercice 3

> p:=n->product(1+k/n^2,k=1..n);

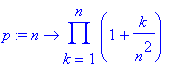
> p(20);

> evalf(%);

> seq(evalf(p(i)),i=1..50);

> evalf(exp(1/2));

> product(1+k/n^2,k=1..n);

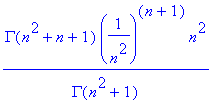
> limit(product(1+k/n^2,k=1..n),n=infinity);

Je suis terrassé...

Exercice 8

> seq(evalf(cos(n)),n=0..50);

> min(seq(evalf(cos(n)),n=0..10)),max(seq(evalf(cos(n)),n=0..10));

> min(seq(evalf(cos(n)),n=0..100));

> min(seq(evalf(cos(n)),n=0..1000));

> Digits:=20;

> min(seq(evalf(cos(n)),n=0..10000));

> min(seq(evalf(cos(n)),n=0..100000));